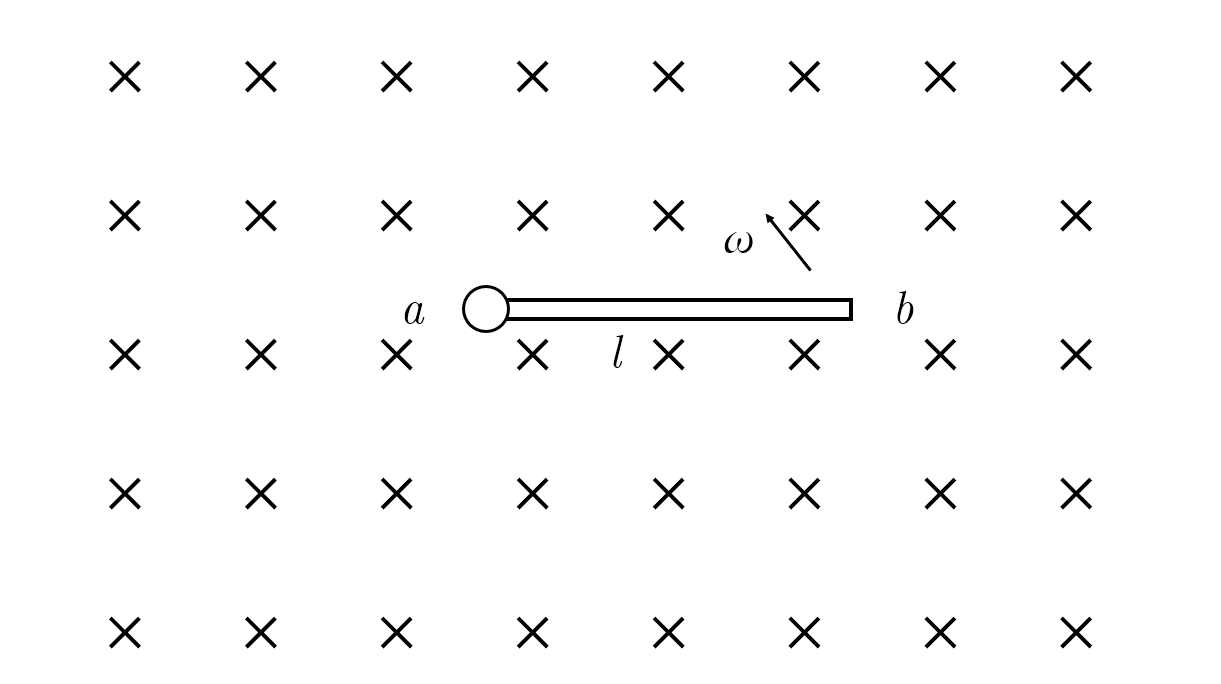没有克服诱惑的我看了《高中数学 选修 2-2》

起因是这样的

物理学到了电磁感应的一套操作

有一个非常经典的问题

在磁感应强度为$B$，垂直于纸面的磁场中，一根长为$l$的直导线绕其一端旋转，导线中的感应电动势是多少？

（图真难画，ppt难受死了，求推荐好的画图的工具）

物理老师：我们用微元法xjb搞搞：

$$ E=\int_0^lB\omega xdx\
$$

然后呢？它等于

$$ \frac 1 2B\omega l^2 $$

至于为什么呢？

等你们学了2-2就知道了

于是我就非常不爽。。。

偷偷看了一波2-2。。。

看了一些骚东西。。

微积分基本定理

比如说，我们现在知道路程关于时间的函数$s=f(t)$

然后我们还知道速度关于时间的函数$v=g(t)$

显然$f’(t)=g(t)$

但是。。如果我要自虐，非要用$g(t)$来表示$f(t)$的话

可以这样搞

$$ f(t_1)-f(t_2)=\int_{t_1}^{t_2}g(t)dt $$

（上面是牛顿的脑洞）

那么这个有什么用呢？

比如说我们要求

$$ \int_{a}^{b}f(x)dx $$

可以先找一个函数$F(x)$，满足$F’(x)=f(x)$，然后就有

$$ \int_{a}^{b}f(x)dx=F(b)-F(a) $$

物理问题

回顾一下刚才的物理问题。。

$$ E=\int_0^lB\omega xdx\
=\left[\frac 1 2B\omega x^2\right]^l_0
=\frac 1 2B\omega l^2 $$

美滋滋

数学问题

感觉自己掌握了不得了的数学武器

看见什么就想积一下

比如这个

$$ \int_0^1x^2dx=\left[\frac 1 3x^3\right]^1_0=\frac 1 3 $$

可把我给牛逼坏了

于是我脑洞大开

能不能算一下圆的面积呢？

不妨考虑圆在第一象限的$\frac 1 4$

有$f(x)=\sqrt{r^2-x^2}\ , \ x\in[0,r]$

我们要求的是这个：

$$ 4\int_0^r\sqrt{r^2-x^2}dx $$

然后。。不会做了

开门，放Mathematica！

Mathematica告诉我这个等于$\pi r^2$

好像很有道理

emmmm

于是上Wolfram Alpha

第一步提示我三角换元

后面的要氪金才可以看qwq

于是。。手推。。。

$$ dx=r\cos \theta d\theta\
4\int_0^r\sqrt{r^2-x^2}dx\
=4r^2\int_0^{\frac \pi 2}\cos^2\theta d\theta\
=2r^2\int_0^{\frac \pi 2}(1+\cos2\theta)d\theta\
=2r^2\left[\theta+\frac{1}{2}\sin 2\theta\right]_{0}^{\frac{\pi}{2}} =\pi r^2 $$

真是伤身体。。

于是我去Wikipedia上看了一波

人家是这样搞的：

使用微积分，我们将圆像洋葱一样分为薄圆环，递增地求出面积。这是二维壳积分法。对“洋葱”以 $t$ 为半径的无穷薄圆环，贡献的面积是 $2πtdt$，周长的长度乘以其无穷小宽度。这样对半径为 $r$ 的圆给出了一个初等积分：

感觉自己是个傻子

又一个物理问题

书上告诉我们，经过理论计算，正弦式交变电流的等效值为$\frac {E_m}{\sqrt 2} $

非常不爽

想一想，如果要满足热量相同的话，应该是求$i^2-t$图象的积分

不妨设$f(x)=\sin^2x$

先考虑半个周期的情况

$$ \int_0^\pi\sin^2xdx\
=\int_0^\pi\left(\frac{1-\cos2x}2\right)dx\
=\int_0^\pi\frac 1 2dx-\int_0^\pi\frac {\cos 2x}{2}dx\
=\frac \pi 2-0\
=\frac \pi 2 $$

考虑普通的直流，产热是$i^2\pi$

所以$i=\frac {1}{\sqrt2}$

啊

舒适qwq