Codeforces Round #428 (Div. 2) C
题目描述
原题地址:Codeforces
一句话题意,有一颗树,对这颗树进行dfs,求dfs路径长度的期望值
思路
第一次做期望的题呢。
期望的定义是$权值\times概率$,就是路径长度乘上走到这个点的概率。
我们可以算出所有叶子节点的深度,乘上到达这些节点的概率。
概率应该怎么求呢?
如图:
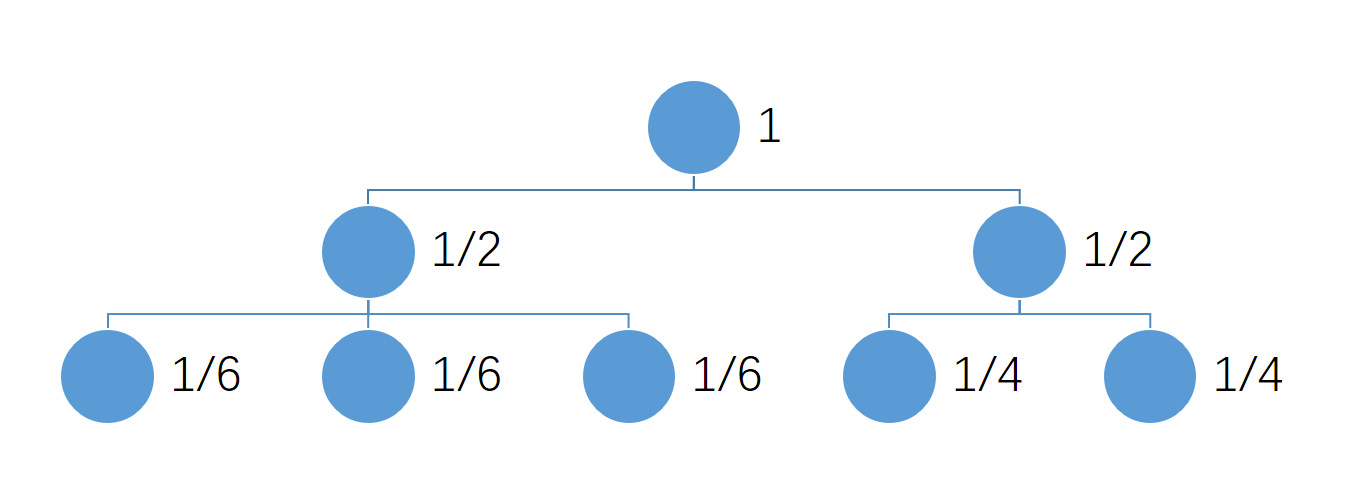
嗯,就是这样,然后算一下就好了。
非常扯的是我比赛的时候WA了,结果今天一看数据是没有保留足够的小数位数。。。
qwq惨。
代码
//
// Created by Margatroid on 2017/8/12.
//
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
vector<int> g[maxn];
void addedge(int f, int t) { g[f].push_back(t), g[t].push_back(f); }
long double ans;
void dfs(int no, int fa, int d, long double p)
{
for (int i = 0; i < g[no].size(); ++i)
{
if (g[no][i] == fa)
continue;
dfs(g[no][i], no, d + 1, p / (g[no].size() - 1));
}
if (g[no].size() == 1)
ans += d * p;
}
int n;
int main()
{
cin >> n;
g[1].push_back(0);
for (int i = 1; i < n; ++i)
{
int u, v;
cin >> u >> v;
addedge(u, v);
}
dfs(1, 0, 0, 1);
cout << fixed << setprecision(10) << ans << endl;
}
最后附送tkz限定表情一张

navigate_before
[Luogu 3919] [毒瘤] 可持久化数组
[APIO2009] 抢掠计划
navigate_next