二项堆与斐波那契堆
book
归档： 联创 
flag
mode_edit

玄妙的数据结构第二弹

斐波那契堆也是一种逃课数据结构，通过延迟操作，使得除了 delete_min, decrease_key 之外的所有操作都实现了均摊 $O(1)$。

二项堆

二项堆由一组二项树组成，记 $n$ 阶的二项树为 $B(n)$，则有：

  • $B(0)$ 为一个节点
  • $B(n)$ 是由两个 $B(n-1)$ 合并而成的二项树

fib-1

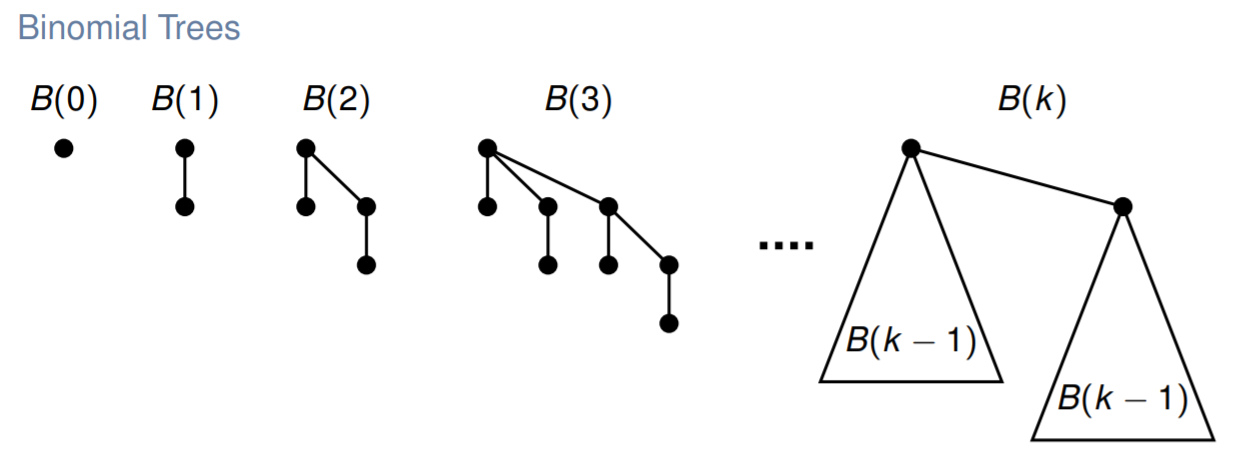
注意到 $k$ 阶二叉堆恰好具有 $k$ 个儿子。

一个二项堆满足：

  • 在这个二项堆的所有二项树中，没有两棵二项树具有相同的阶

下图是一个合法的二项堆

fib-2

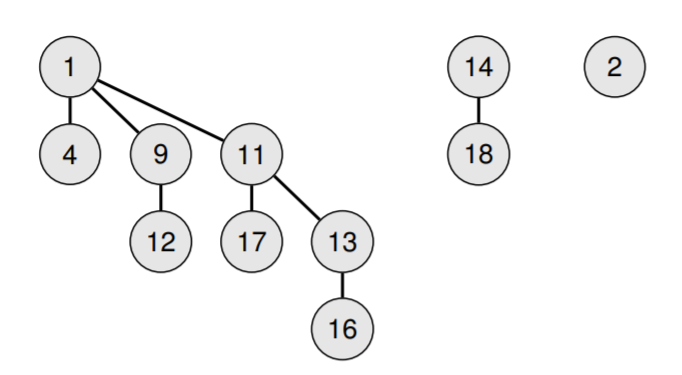
二项堆可以实现高效（$O(\log n)$）合并。具体操作就是不断地合并具有相同阶的二项树，直到所有二项树都具有不同的阶。

斐波那契堆

二项堆太菜了。

它为什么菜呢？因为它太急（Eager）了。斐波那契堆之所以实现了如此玄幻的复杂度，是因为它推后了很多操作。

构造

斐波那契堆由一系列小根堆组成，这些小根堆的根节点存放在一个双向循环链表里面，我们维护一根 min 指针，指向这个链表里最小的元素。

fib-3

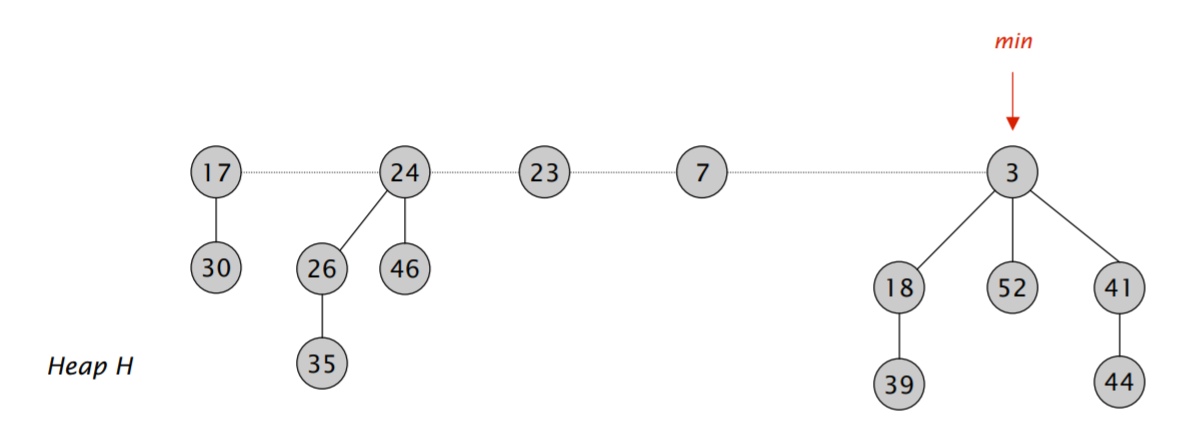
（如果要实现 decrease_key 的话，需要给节点打标记，但是由于我没有实现这个，因此就没打）

操作

插入

插入一个值，只需要把它放进根节点的双向循环列表里，然后更新 min 指针（如果有必要）。

复杂度显然是 $O(1)$

查询最小值

读出 min 指针指向的数即可，也是 $O(1)$

删除最小值

首先，我们将 min 指针指向的元素删除，然后将它的儿子全部合并进根节点的双向循环链表里。然后开始执行类似二项堆合并的操作：不断合并具有相同阶数的小根堆，直到根节点列表里的所有小根堆都具有不同的阶。

fib-4

fib-5

fib-6fib-7

fib-8

fib-9

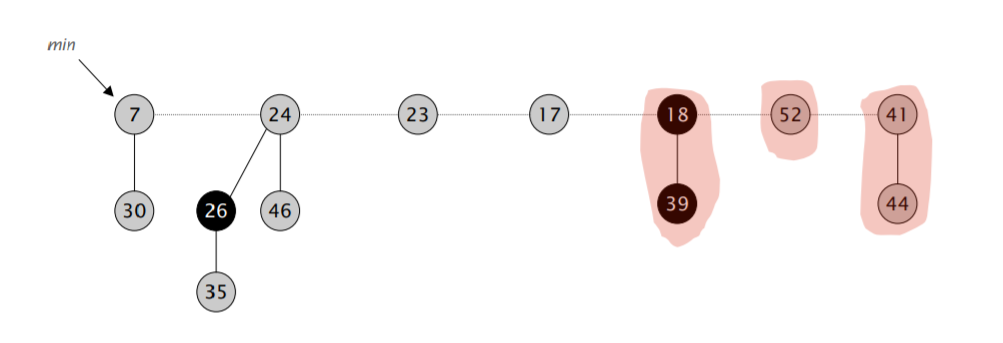
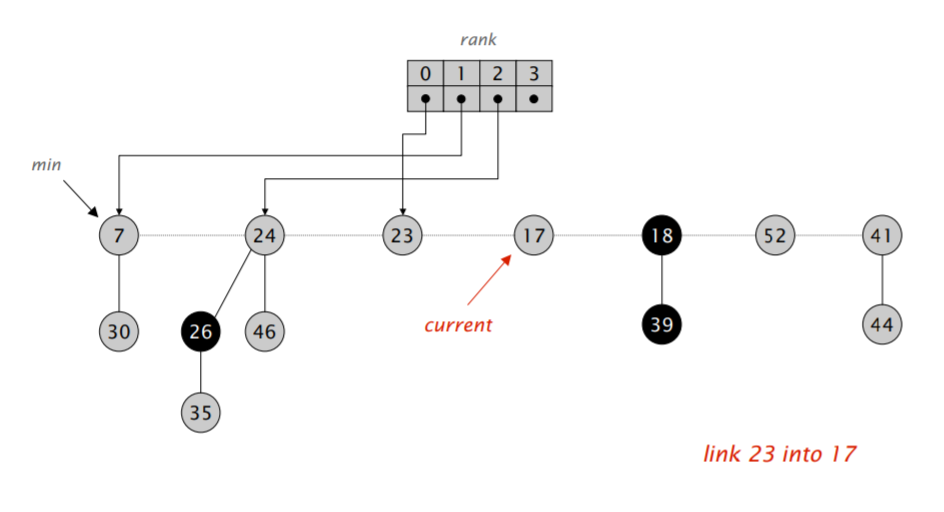
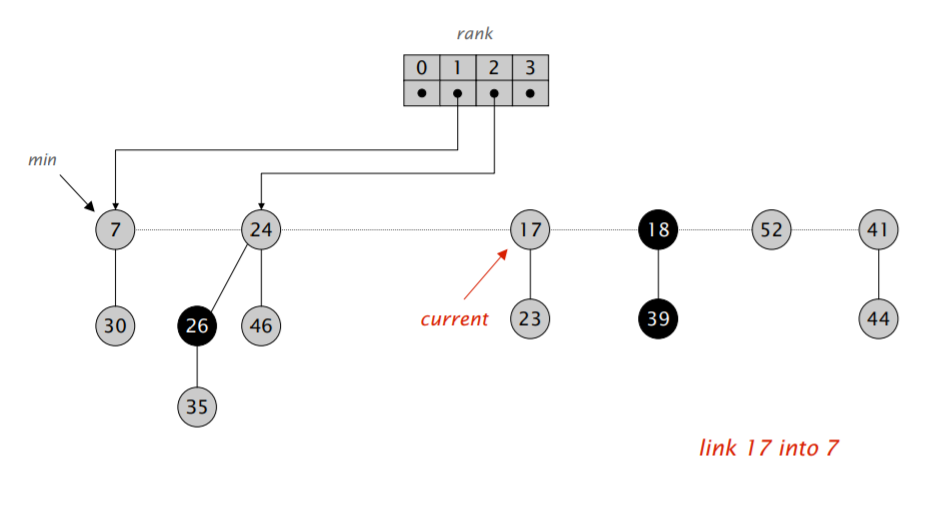
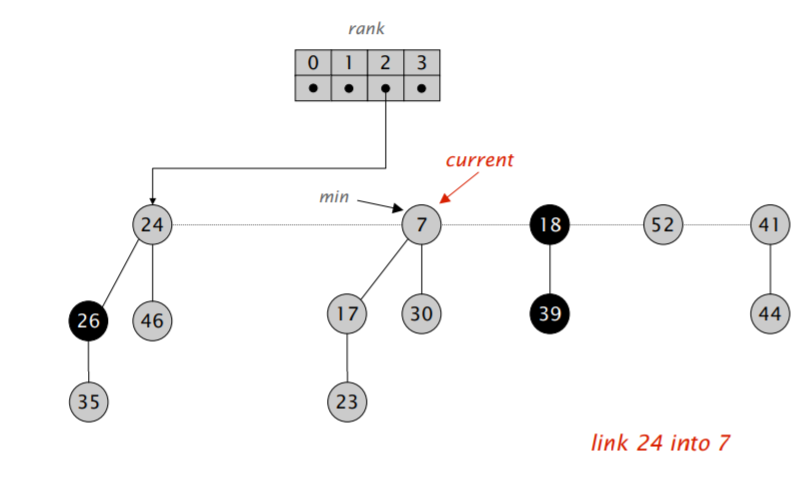
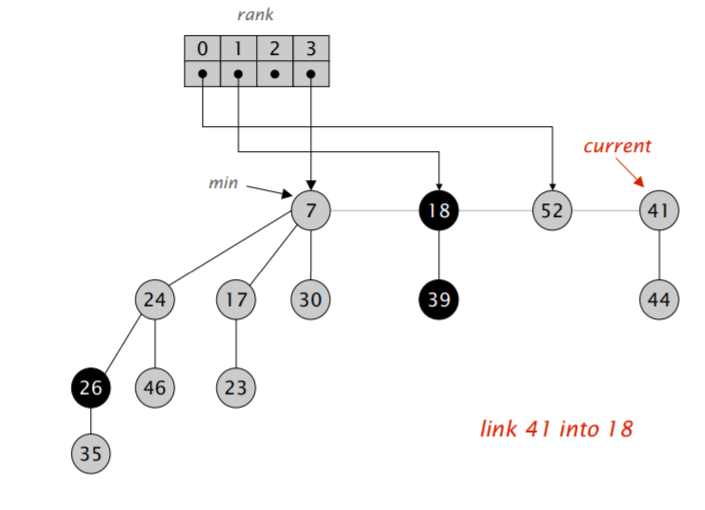
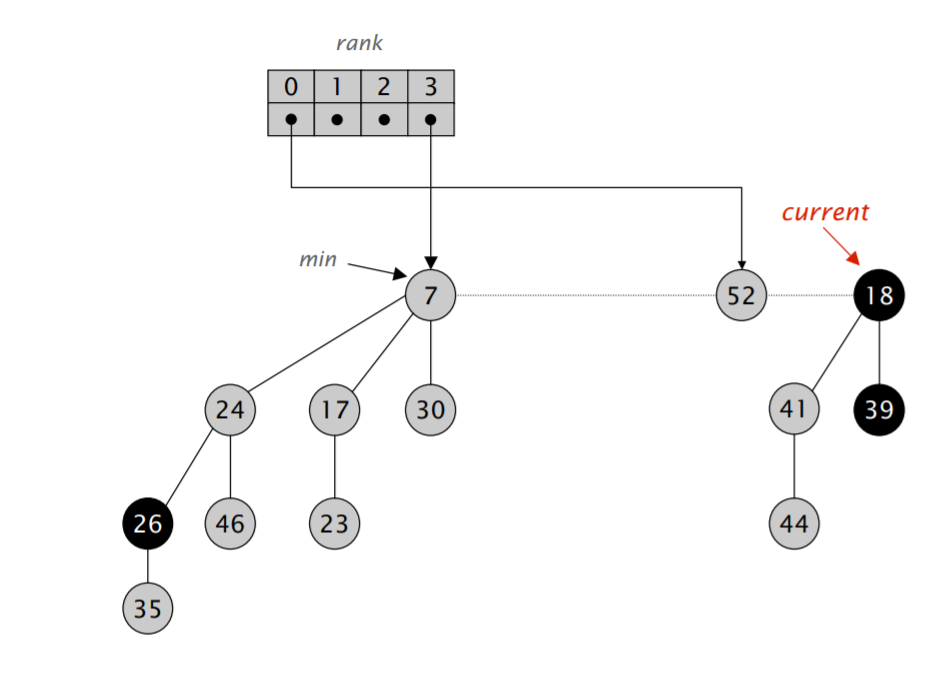
难点在于「合并树，直到任意两棵树都具有不同的阶」。我们需要遍历一遍链表，对于每次遍历拿到的元素，我们可以检查对应的 rank 数组里是不是空的，如果不是，那就进行合并，并检测合并后的堆对应的 rank 数组里是不是空的，再重复以上流程，算导的伪代码如下：

fib-10

注意到在遍历过程中，$w$ 可能会发生变化，因此需要在进入第二层循环前先保存一下下一个应该访问的节点的地址。

template<typename Key, typename Compare>
void PriorityQueue<Key, Compare>::merge_tree(PriorityQueue::Node *smaller, PriorityQueue::Node *bigger) {
  // remove bigger from list, then make bigger one the child of smaller

  // remove bigger
  auto bp = bigger->prev, bn = bigger->next;
  bp->next = bn;
  bn->prev = bp;

  // merge as child
  if (smaller->child) {
    auto cp = smaller->child->prev, c = smaller->child;
    cp->next = bigger;
    bigger->next = c;
    c->prev = bigger;
    bigger->prev = cp;
    bigger->parent = smaller;
  } else {
    bigger->next = bigger->prev = bigger;
    bigger->parent = smaller;
    smaller->child = bigger;
  }
  ++(smaller->deg);
}

template<typename Key, typename Compare>
typename PriorityQueue<Key, Compare>::Node *
PriorityQueue<Key, Compare>::extract_min() {
  Node *p = min_element_;
  if (min_element_->next == min_element_) {
    min_element_ = nullptr;
  } else {
    auto mn = min_element_->next, mp = min_element_->prev;
    min_element_ = mn;
    mp->next = mn;
    mn->prev = mp;
  }
  p->prev = p->next = p;
  return p;
}

template<typename Key, typename Compare>
void PriorityQueue<Key, Compare>::consolidate() {
  Node *cons[256];
  std::fill(std::begin(cons), std::end(cons), nullptr);
  Node *x, *y;
  while (min_element_) {
    x = extract_min();
    int d = x->deg;
    while (cons[d]) {
      y = cons[d];
      if (cmp_(y->key, x->key))
        std::swap(x, y);
      merge_tree(x, y);
      cons[d] = nullptr;
      ++d;
    }
    cons[d] = x;
  }

  for (auto &con : cons)
    if (con)
      con->prev = con->next = con;
  min_element_ = nullptr;
  for (auto &con : cons) {
    if (con) {
      if (min_element_ == nullptr) {
        min_element_ = con;
      } else {
        auto mn = min_element_->next;
        min_element_->next = con;
        con->next = mn;
        mn->prev = con;
        con->prev = min_element_;
        con->parent = nullptr;
        if (cmp_(con->key, min_element_->key))
          min_element_ = con;
      }
    }
  }
}

实现

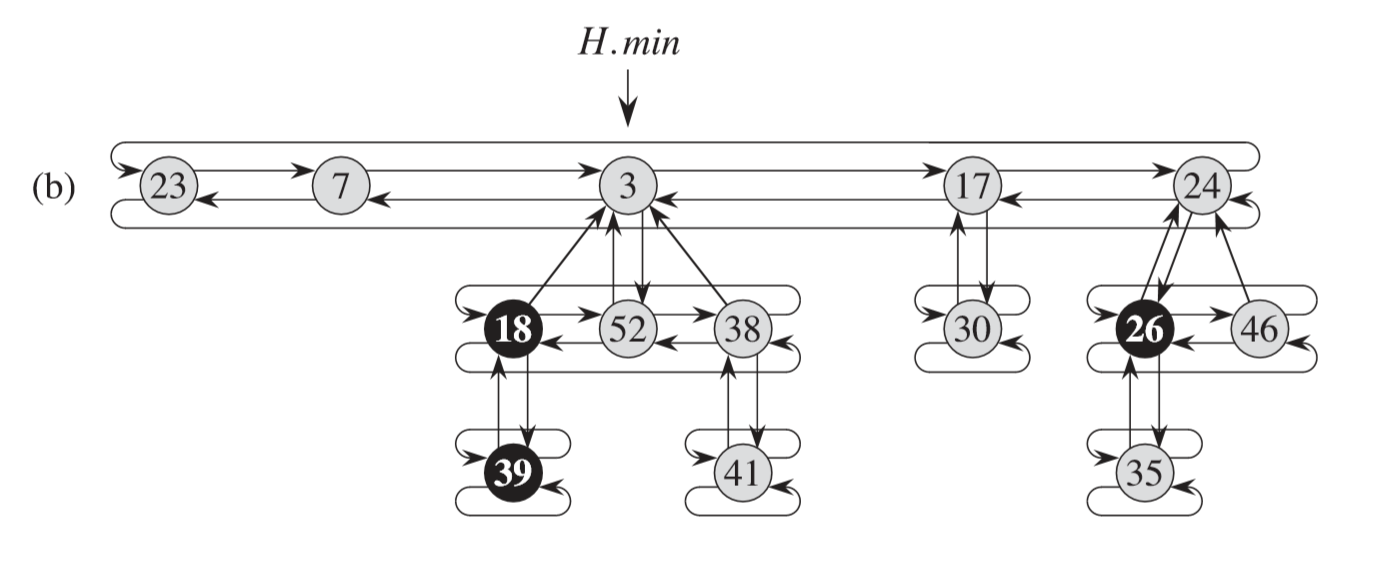
实际上，我们的堆的每一层都是一个双向循环链表：对于多叉树，我们只在父节点里保存了第一个元素的地址，而父节点的所有儿子都保存在一个双向循环链表中：

fib-11

Reference

数据结构 堆
navigate_before navigate_next