我也是会写平衡树的人了
二叉查找树(BST)
二叉查找树具有很多很妙的性质:
对于每一个节点,满足左子树的所有值小于该节点的值小于右子树的所有节点的值
由 1. ,若我们将一棵二叉查找树进行中序遍历,那么可以得到一个有序序列
由 1. 2.,考虑如何将有序序列重建为一棵二叉查找树:我们应当首先在区间内找到一个节点作为根节点,然后对于该节点左右两侧的序列递归执行相同的建树操作。考虑「找到一个节点的」过程,实际上选取方式足足有 $n$ 种,而且他们产生的树一定不同,因此:对于同一序列,存在多种合法的二叉查找树。
由 3. ,考虑二叉查找树的形态,若每次选择区间中点,那么最后会得到一棵相对平衡的树;若每次选择区间左端点,则会得到一条长链。
二叉查找树可以快速确定元素 $x$ 是否在树内。考虑二叉查找树的查找过程:首先将 $x$ 与树根比较,如果 $x< \mathit{root}$,那么 $x$ 一定在左子树内;同样的,若 $x=root$,那么 $x$ 就是根节点;对于 $x>\mathit{root}$,那么 $x$ 在右子树内。递归在左右子树内应用这个过程,即可完成查找。
考虑 5. 中过程的时间复杂度,为 $O(\mathit{height})$,由 4. 若树为一条长链,那么时间复杂度为 $O(n)$;若树为一棵平衡的树,那么时间复杂度为 $O(\log n)$。
考虑二叉查找树的插入过程,若要将 $x$ 插入树中,首先和插入操作一样,比较 $x$ 和根的大小,如果 $x<\mathit{root}$ 那么将左子树替换为插入后的树,反之替换右子树。而边界条件为:向空树中插入一个值,得到一个节点。
对于 7. 中的插入过程,我们注意到树的形态是不受我们控制的,如果我们插入 $1,2,3,4,5,6\cdots n$,那么树就会退化成一条链。因此,我们需要一种能够维持树的平衡性的数据结构,这就是平衡树。
Treap
如果我们在二叉搜索树的每个节点上额外存储一个值,使得对于这个值,整棵二叉搜索树还满足堆性质:每个节点的关键值大于左右儿子的关键值。然后在新建节点时随机生成一个关键值,就可以使得整棵树期望平衡。
带有旋转操作的数据结构都难以可持久化,既然要用 Haskell 写,就只能写那些可以高效地可持久化的东西——无旋 Treap。
data Treap a = Node Int a Int (Treap a) (Treap a) | Nil deriving Show -- Size Value Key lc rc
getSize :: Treap a -> Int
getSize Nil = 0
getSize (Node sz _ _ _ _) = sz
无旋 Treap 的操作基于分裂和合并。分裂操作可以依据 $v$ 把整棵树分裂为左右两部分:左半边所有节点的值 $\leq v$,右半边所有节点的值 $>v$。而合并是分裂的逆过程,可以将两个值域不重合的 Treap 合并为一个大的 Treap。
分裂
考虑怎样才能以 $\mathit{value}$ 为界把一个 Treap 分裂为两块呢?
不妨设分裂后我们得到了 $lc$ 与 $rc$ 。首先拿着 $\mathit{value}$ 与根节点的 $v$ 进行比较, 如果 $v\leq \mathit{value}$ ,那么根节点连同左子树都应该是属于 $lc$ 的。这样,我们需要继续分裂右子树,右子树可以被分裂为两块:$rlc$ 与 $rrc$ 。由图可知,我们可以把 $rlc$ 当成 $lc$ 的右子树,$rrc$ 自成一派,成为 $rc$。
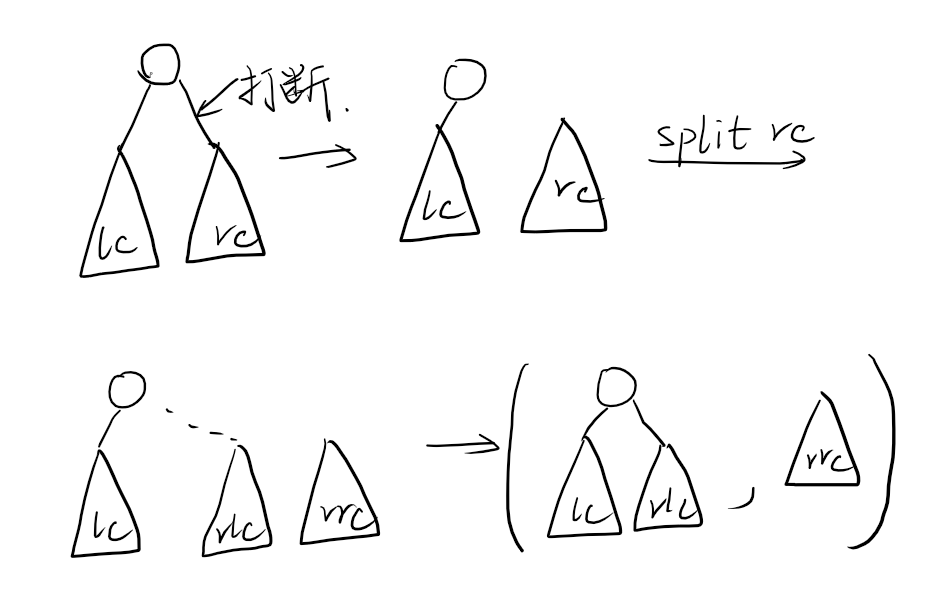
同理可以这样处理 $v>\mathit{value}$ 的情况,代码见下:
split :: (Num a, Ord a) => Treap a -> a -> (Treap a, Treap a)
split Nil _ = (Nil, Nil)
split (Node _ v key lc rc) value
| v <= value = (Node (getSize l1 + getSize lc + 1) v key lc l1, r1)
| otherwise = (l2, Node (getSize r2 + getSize rc + 1) v key r2 rc)
where
(l1, r1) = split rc value
(l2, r2) = split lc value
合并
考虑该如何合并两个值域不重叠的 Treap 呢?
似乎拿着其中一个去和另一个的一棵子树合并即可。不妨设我们要合并 $lc$ 与 $rc$,且 $\max{lc} < \min{rc}$ 。那么我们可以拿着 $lc$ 的右子树与 $rc$ 合并,也可以拿着 $rc$ 的左子树和 $lc$ 合并,都满足「值域不重叠」 的性质。那么我们究竟该拿哪一个呢?这时候就要拿出堆性质了,这里我们实现大根堆,比较两个根节点的 $key$ 值,较小的一个就只能和另一个的子树合并了。
infixl 5 ><
(><) :: (Num a, Ord a) => Treap a -> Treap a -> Treap a
Nil >< u = u
u >< Nil = u
u@(Node _ v1 k1 llc lrc) >< v@(Node _ v2 k2 rlc rrc)
| k1 <= k2 = Node (getSize rrc + getSize l + 1) v2 k2 l rrc
| otherwise = Node (getSize llc + getSize r + 1) v1 k1 llc r
where
l = u >< rlc
r = lrc >< v
基本操作
有了分裂和合并,我们的生活就改善了很多。如果要插入一个值 $v$ ,可以先把树以 $v$ 为界分裂成两部分 $lc, rc$,然后再按照 $lc,v,rc$的顺序合并起来。
insert :: (Num a, Ord a) => Treap a -> a -> Int -> Treap a
insert tr v num = l >< t >< r
where
(l, r) = split tr v
t = Node 1 v num Nil Nil
删除稍微复杂一点,考虑到普通平衡树这个题里面,一个值可以出现多次,删除单个值 $v$ 是比较复杂的。我们可以这样操作:
- 首先分裂出来一棵树,这棵树里包含了原树里的所有 $v$ 。
- 将这棵树的左右子树合并,丢掉根节点。
- 将这棵树与之前的分裂出来的片段合并,得到结果
第一步操作比较复杂,可以这样进行:首先按照 $v$ 把整棵树分裂为 $(lc,rc)$,然后再以 $v-1$ 为界分裂 $lc$ 得到 $(_,lrc)$,这样,$lrc$ 就是我们想要的树了。代码见下:
erase :: (Num a, Ord a) => Treap a -> a -> Treap a
erase Nil _ = error "Cannot erase a empty Treap"
erase tr v = ll >< ntr >< r
where
(l, r) = split tr v
(ll, Node _ _ _ rlc rrc) = split l (v - 1)
ntr = rlc >< rrc
求 $v$ 的排名自然也不复杂,我们只需要以 $v-1$ 为界,得到 $\leq v-1$ 的值的数目即可。
求第 $k$ 大的操作也不复杂,只需要在比较左子树的 $size$ 的同时不断递归就可以了。
以上两个操作的代码见下:
rank :: (Num a, Ord a) => Treap a -> a -> Int
rank Nil _ = error "Cannot rank a empty Treap"
rank tr v = getSize l + 1
where
(l, _) = split tr (v - 1)
kth :: (Num a, Ord a) => Treap a -> Int -> a
kth Nil _ = error "Cannot kth a empty Treap"
kth (Node _ v _ lc rc) k
| lsz + 1 == k = v
| lsz < k = kth rc (k - lsz - 1)
| otherwise = kth lc k
where
lsz = getSize lc
由于元素可重复,求前驱和后继的代码稍微有一点复杂,实际上是写成循环比较好。思路是这样的,在求前驱的时候,如果遇到一个比 $v$ 更小的元素,就先记下来,再向右边走,看看能不能碰到更大、但是小于 $v$ 的元素。求后继同理。这里放 C++ 的代码。
int prev(node* tr, int value) {
int res;
while (tr) {
if (tr->value < value)
res = tr->value, tr = tr->rc;
else
tr = tr->lc;
}
return res;
}
int succ(node* tr, int value) {
int res;
while (tr) {
if (tr->value > value)
res = tr->value, tr = tr->lc;
else
tr = tr->rc;
}
return res;
}
代码(普通平衡树)
Haskell
{-# OPTIONS_GHC -O2 #-}
-- {-# LANGUAGE Strict #-}
module Main where
import Prelude hiding (succ)
import Data.Char (digitToInt, isSpace)
import Text.Printf (printf)
import qualified Data.Text as T
import qualified Data.Text.IO as I
data Treap a = Node Int a Int (Treap a) (Treap a) | Nil deriving Show -- Size Value Key lc rc
getSize :: Treap a -> Int
getSize Nil = 0
getSize (Node sz _ _ _ _) = sz
split :: (Num a, Ord a) => Treap a -> a -> (Treap a, Treap a)
split Nil _ = (Nil, Nil)
split (Node _ v key lc rc) value
| v <= value = (Node (getSize l1 + getSize lc + 1) v key lc l1, r1)
| otherwise = (l2, Node (getSize r2 + getSize rc + 1) v key r2 rc)
where
(l1, r1) = split rc value
(l2, r2) = split lc value
infixl 5 ><
(><) :: (Num a, Ord a) => Treap a -> Treap a -> Treap a
Nil >< u = u
u >< Nil = u
u@(Node _ v1 k1 llc lrc) >< v@(Node _ v2 k2 rlc rrc)
| k1 <= k2 = Node (getSize rrc + getSize l + 1) v2 k2 l rrc
| otherwise = Node (getSize llc + getSize r + 1) v1 k1 llc r
where
l = u >< rlc
r = lrc >< v
insert :: (Num a, Ord a) => Treap a -> a -> Int -> Treap a
insert tr v num = l >< t >< r
where
(l, r) = split tr v
t = Node 1 v num Nil Nil
erase :: (Num a, Ord a) => Treap a -> a -> Treap a
erase Nil _ = error "Cannot erase a empty Treap"
erase tr v = ll >< ntr >< r
where
(l, r) = split tr v
(ll, Node _ _ _ rlc rrc) = split l (v - 1)
ntr = rlc >< rrc
rank :: (Num a, Ord a) => Treap a -> a -> Int
rank Nil _ = error "Cannot rank a empty Treap"
rank tr v = getSize l + 1
where
(l, _) = split tr (v - 1)
kth :: (Num a, Ord a) => Treap a -> Int -> a
kth Nil _ = error "Cannot kth a empty Treap"
kth (Node _ v _ lc rc) k
| lsz + 1 == k = v
| lsz < k = kth rc (k - lsz - 1)
| otherwise = kth lc k
where
lsz = getSize lc
prev' :: Ord a => Treap a -> a -> a -> a
prev' Nil _ res = res
prev' (Node _ v _ lc rc) vl res
| v < vl = prev' rc vl v
| otherwise = prev' lc vl res
prev :: (Num a, Ord a) => Treap a -> a -> a
prev tr v = prev' tr v 0
succ' :: Ord a => Treap a -> a -> a -> a
succ' Nil _ res = res
succ' (Node _ v _ lc rc) vl res
| v > vl = succ' lc vl v
| otherwise = succ' rc vl res
succ :: (Num a, Ord a) => Treap a -> a -> a
succ tr v = succ' tr v 0
int :: String -> Int
int str = int' (filter (not . isSpace) str) 0
where
int' [] x = x
int' ('-':xs) _ = -1 * (int' xs 0)
int' (x:xs) p = int' xs $ p * 10 + digitToInt x
repM :: Monad m => Int -> a -> (a -> m a) -> m a
repM 0 x _ = return x
repM n x f = f x >>= \y -> repM (n - 1) y f
repM_ :: Monad m => Int -> a -> (a -> m a) -> m ()
repM_ n x f = repM n x f >> return ()
main :: IO ()
main = do
n <- int <$> T.unpack <$> I.getLine
repM_ n (Nil, 0) $ \(root, seed) -> do
[op, num] <- map (int . T.unpack) . T.words <$> I.getLine
let res = (1919 * seed * seed + 19260817 * seed + 2333) `mod` 1000000007
case op of 1 -> return $ (insert root num res, res)
2 -> return $ (erase root num, res)
3 -> printf "%d\n" (rank root num) >> return (root, res)
4 -> printf "%d\n" (kth root num) >> return (root, res)
5 -> printf "%d\n" (prev root num) >> return (root, res)
6 -> printf "%d\n" (succ root num) >> return (root, res)
_ -> error "???"
return ()
C++
#include <bits/stdc++.h>
using namespace std;
namespace mgt {
struct node {
int value, key, size; // key is for heap
node *lc, *rc;
node(int value) {
this->value = value;
lc = rc = 0;
size = 1;
key = rand();
}
};
using pnns = pair<node*, node*>;
const int maxn = (int)1e6 + 10;
node* newNode(int value) { return new node(value); }
void updateSize(node* tr) {
if (tr)
tr->size = 1;
else
return;
if (tr->lc)
tr->size += tr->lc->size;
if (tr->rc)
tr->size += tr->rc->size;
}
int getSize(node* tr) { return tr == 0 ? 0 : tr->size; }
pnns split(node* tr, int value) { // get 2 trees: forall node in fst, node.value
// <= value, vice versa for snd
if (tr == nullptr)
return pnns(nullptr, nullptr);
if (tr->value <= value) {
auto x = split(tr->rc, value);
tr->rc = x.first;
updateSize(tr);
return pnns(tr, x.second);
} else {
auto x = split(tr->lc, value);
tr->lc = x.second;
updateSize(tr);
return pnns(x.first, tr);
}
}
node* merge(node* u, node* v) { // make sure max(u.value) <= min(v.value)
if (!(u && v))
return u == 0 ? v : u;
if (u->key <= v->key) {
v->lc = merge(u, v->lc);
updateSize(v);
updateSize(u);
return v;
} else {
u->rc = merge(u->rc, v);
updateSize(u);
updateSize(v);
return u;
}
}
node* insert(node* tr, int value) {
auto x = split(tr, value);
auto t = newNode(value);
return merge(x.first, merge(t, x.second));
}
node* erase(node* tr, int value) {
auto x = split(tr, value);
auto y = split(x.first, value - 1);
auto z = merge(y.second->lc, y.second->rc);
return merge(y.first, merge(z, x.second));
}
int getRank(node* tr, int value) {
auto tmp = split(tr, value - 1);
int res = getSize(tmp.first) + 1;
merge(tmp.first, tmp.second);
return res;
}
int find(node* tr, int rank) {
if (getSize(tr->lc) + 1 == rank)
return tr->value;
if (getSize(tr->lc) < rank)
return find(tr->rc, rank - getSize(tr->lc) - 1);
return find(tr->lc, rank);
}
int prev(node* tr, int value) {
int res;
while (tr) {
if (tr->value < value)
res = tr->value, tr = tr->rc;
else
tr = tr->lc;
}
return res;
}
int succ(node* tr, int value) {
int res;
while (tr) {
if (tr->value > value)
res = tr->value, tr = tr->lc;
else
tr = tr->rc;
}
return res;
}
template <class T> inline T gn() {
register int k = 0, f = 1;
register char c = getchar();
for (; !isdigit(c); c = getchar())
if (c == '-')
f = -1;
for (; isdigit(c); c = getchar())
k = k * 10 + c - '0';
return k * f;
}
} // namespace mgt
using mgt::gn;
int main() {
int n = gn<int>();
mgt::node* root = nullptr;
for (int i = 1; i <= n; ++i) {
int op = gn<int>();
if (op == 1)
root = mgt::insert(root, gn<int>());
else if (op == 2)
root = mgt::erase(root, gn<int>());
else if (op == 3)
printf("%d\n", mgt::getRank(root, gn<int>()));
else if (op == 4)
printf("%d\n", mgt::find(root, gn<int>()));
else if (op == 5)
printf("%d\n", mgt::prev(root, gn<int>()));
else if (op == 6)
printf("%d\n", mgt::succ(root, gn<int>()));
}
}