本来试图用 Haskell 写个配对堆水过(毕竟这个东西复杂度这么好看)洛谷的【模板】堆来着,结果竟然把各种堆写了一个遍…
以下讨论的堆都是小根堆
配对堆
均摊复杂度优秀的数据结构都是逃课数据结构,下面我们来欣赏一下配对堆的逃课思路:
说到配对堆的结构,首先要介绍一下配对树,一棵配对树是这样的:它有一个 val :存储值,和一个列表:存放配对树作为子树。而一个配对堆要么是空的,要么是一棵配对树。写成 Haskell 如下:
data ParingTree a = ParingTree a [ParingTree a]
data ParingHeap a = Empty | ParingHeap (ParingTree a)
findMin
和所有的堆一样,取最小值是 $O(1)$ 的,只需要拿出配对树的根存储的值即可。
findMin :: (Ord a) => ParingHeap a -> a
findMin Empty = error "Cannot access an empty heap"
findMin (ParingHeap t) = val t
merge
配对堆是可以合并的。而且合并的复杂度是 $O(1)$,这是一个令人感到不可思议的复杂度。我们来鉴赏一下这里应该怎么逃课:首先,一个非空堆和空堆合并得到非空堆本身。那么考虑两个非空堆的合并:我们只需要把根节点值较大的一个扔到另一个的子树列表里就可以了。正确性可以自行考虑堆的性质。
(这个课逃的怎么样xxx)
(><) :: (Ord a) => ParingHeap a -> ParingHeap a -> ParingHeap a
Empty >< v = v
u >< Empty = u
l@(ParingHeap u) >< r@(ParingHeap v)
| val u < val v = ParingHeap (ParingTree (val u) (v:(subHeaps u)))
| otherwise = r >< l
insert
插入也是 $O(1)$ 的,因为往某个堆里插入一个数 $v$ ,相当于把 一个只有一个数 $v$ 的堆和原来的堆合并起来。
infixl 5 <|
(<|) :: (Ord a) => ParingHeap a -> a -> ParingHeap a
tr <| val = tr >< ParingHeap (ParingTree val [])
deleteMin
逃课是要还的。
删除最小值,相当于把堆的根节点扔掉。那么需要把根节点的子树列表里的子树合并成一个新堆,该怎么做呢?啊,合并!合并我会啊,单次复杂度 $O(1)$!考虑子树列表 $t_1,t_2,t_3\cdots t_n$,如果我们从左往右合并,依次得到 $t_{12},t_{123},t_{1234}\cdots t_{123\cdots n}$ 好像成功了!
但是到合并完之后的堆的形态:相当于把一条长蛇接到了 $t_1$ 的后面,非常不优。
这就是「配对」二字的由来:首先从左到右,一对一对地(?我为啥要学这种现充数据结构)合并子树,然后再从右向左,把它们合并成一个大的堆:先合并成 $t_{12},t_{34},t_{56}\cdots t_{(n-1)n}$,然后再从右向左合并回去。这个操作写成代码是这样的:
mergePairs :: (Ord a) => [ParingTree a] -> ParingHeap a
mergePairs [] = Empty
mergePairs [t] = ParingHeap t
mergePairs (x:y:xs) = (ParingHeap x >< ParingHeap y) >< (mergePairs xs)
用上这个,我们就可以删除最小值了:
deleteMin :: (Ord a) => ParingHeap a -> ParingHeap a
deleteMin Empty = error "Cannot delete anything from empty heap"
deleteMin (ParingHeap (ParingTree _ prs)) = mergePairs prs
遗憾的是,这些代码在洛谷喜提 30 分,体验极差。
斜堆
斜堆是玄学数据结构…它就是一个随机堆加上一些玄学移动,每次合并的时候交换左右子树,喜提 30 分也是意料之中
{-# OPTIONS_GHC -O2 #-}
-- {-# language Strict #-}
module Main where
import Data.Char (digitToInt, isSpace)
import Text.Printf (printf)
import qualified Data.Text as T
import qualified Data.Text.IO as I
repM :: Monad m => Int -> a -> (a -> m a) -> m a
repM 0 x _ = return x
repM n x f = f x >>= \y -> repM (n - 1) y f
repM_ :: Monad m => Int -> a -> (a -> m a) -> m ()
repM_ n x f = repM n x f >> return ()
int :: String -> Int
int str = int' (filter (not . isSpace) str) 0
where
int' [] x = x
int' ('-':xs) _ = -1 * (int' xs 0)
int' (x:xs) p = int' xs $ p * 10 + digitToInt x
data Heap a = Empty | Heap a (Heap a) (Heap a)
val :: (Ord a) => Heap a -> a
val (Heap v _ _ ) = v
findMin :: (Ord a) => Heap a -> a
findMin Empty = error "Cannot access an empty heap"
findMin (Heap t _ _) = t
infixl 5 ><
(><) :: (Ord a) => Heap a -> Heap a -> Heap a
Empty >< v = v
u >< Empty = u
u@(Heap uval ulc urc) >< v@(Heap vval vlc vrc)
| uval < vval = Heap uval (urc >< v) (ulc)
| otherwise = v >< u
infixl 5 <|
(<|) :: (Ord a) => Heap a -> a -> Heap a
tr <| val = tr >< Heap val Empty Empty
deleteMin :: (Ord a) => Heap a -> Heap a
deleteMin Empty = error "Cannot delete anything from empty heap"
deleteMin (Heap _ lc rc) = lc >< rc
main :: IO ()
main = do
n <- int <$> T.unpack <$> I.getLine
repM_ n (Empty) $ \(root) -> do
(x:xs) <- map (int . T.unpack) . T.words <$> I.getLine
case x of 1 -> do
let n:[] = xs
return (root <| n)
2 -> printf "%d\n" (findMin root) >> return (root)
3 -> return (deleteMin root)
_ -> error "nmsl"
左偏树
嗯…我拿这个过的这个题。左偏树的常数是真的小。左偏树的思路也是基于合并的。首先介绍一下左偏树的相关定义。
首先假设我们手里有一棵二叉树,如果我们想让他变成满(full)二叉树(除了叶子之外的节点都有左右子树),只需要给所有叶子补上两个节点,给只有一个子树的再补上一个子树。
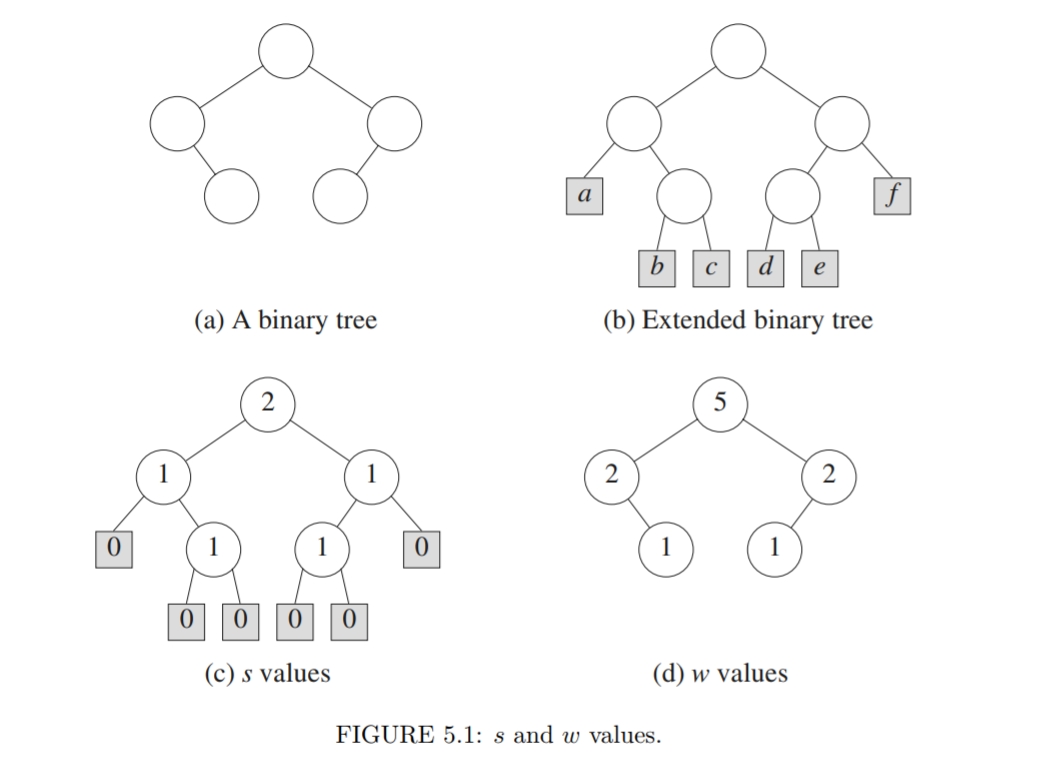
那么原来的节点叫做「内节点」,新加上的(深色方框)叫做外节点。定义 … 算了不想写了,建议直接去看 paper,它写的比我详细的多。
合并的时候通过比较 distance,让树满足左偏性质。删除一个数的时候直接将树的左右子树合并。
data Heap a = Empty | Heap a Int (Heap a) (Heap a)
dis :: Heap a -> Int
dis Empty = 0
dis (Heap _ v _ _) = v
val :: (Ord a) => Heap a -> a
val Empty = error "empty heap has no value"
val (Heap v _ _ _) = v
findMin :: (Ord a) => Heap a -> a
findMin Empty = error "Cannot access an empty heap"
findMin (Heap t _ _ _) = t
infixl 5 ><
(><) :: (Ord a) => Heap a -> Heap a -> Heap a
Empty >< v = v
u >< Empty = u
u@(Heap uval udis ulc urc) >< v@(Heap vval vdis vlc vrc)
| uval <= vval = let x = urc >< v in
if dis ulc < dis x
then Heap uval (dis ulc + 1) x ulc
else Heap uval (dis x + 1) ulc x
| otherwise = v >< u
infixl 5 <|
(<|) :: (Ord a) => Heap a -> a -> Heap a
tr <| val = tr >< Heap val 1 Empty Empty
deleteMin :: (Ord a) => Heap a -> Heap a
deleteMin Empty = error "Cannot delete anything from empty heap"
deleteMin (Heap _ _ lc rc) = lc >< rc