一个*单子*（Monad）说白了不过就是*自函子*范畴上的一个*幺半群*而已，有什么难以理解的。

Philip Wadler

范畴论

我们先了解一些比较数学的东西。。

范畴（Category）

一个范畴包含：

一些东西O(Object)
两个东西间的关系，箭头~>(态射)

一些属性

一定有一个叫 id 的箭头，也叫做 1
箭头可以组合

认识一些范畴

示例图

就是这张图，我们可以看到，object有A,B,C，A到B的箭头是$f$，B到C的箭头是$g$，用$\cdot$表示箭头组合，那么A到C的箭头就是$f\cdot g$

Hask

Haskell 类型系统范畴叫做 Hask

在 Hask 范畴上：

东西是类型
箭头是类型的变换，即 ->
id 就是 id 函数的类型 a -> a
compose 当然就是函数组合的类型

函子（Functor）

我们之前对Functor的理解是行为像容器的类型，不过，在开始之前，请让我们先忘掉它。

我们注意到，在一个范畴内，各个对象之间关系/映射叫做箭头

如果我们有一个更“大”的范畴——以我们刚刚讨论的那种范畴为对象的范畴，那么，这些对象之间的映射/关系就叫做Functor

换句话说，Functor就是范畴与范畴间的映射

认识一些函子

List

这个是容易理解的，比如，你现在有一个list：[a]，而它是范畴中的一个对象。

如果有另一个List：[b]，而且有一个函数可以把[a]映射到[b]，也就是[a] -> [b]，不就是fmap嘛！

这里fmap就是箭头

自函子

自函子比较特殊：它连接相同范畴的 Functor

它有点像上面图示里的id。

举个例子吧，以全体实数为范畴的对象，箭头为小于等于，那么，我们可以获得类似这样的范畴：

自函子

如果我们有一个单调递增的函数$f(x)$，那么这个函数不仅是函子，而且是自函子。

Applicative Functors

首先我们来看看它的定义

class (Functor f) => Applicative f where
    pure :: a -> f a
    (<*>) :: f (a -> b) -> f a -> f b

~~令人头疼的操作.jpg~~

先不管它好了

一个Applicative Functor首先要是一个Functor，我们来慢慢看。

首先pure函数似乎没啥用处，就是把一个东西包进了Functor里。

而<*>就比较蛇，这个东西是一个中缀的运算符，作用。。是把一个包在Functor里的函数应用到另一个Functor里。

比如说

ghci> pure (+42) <*> Just 1
Just 43
ghci> pure (++"qwq") <*> Just "233"
Just "233qwq"
ghci> pure (+) <*> Just 4 <*> Just 9
Just 13

有一张异常形象的图：

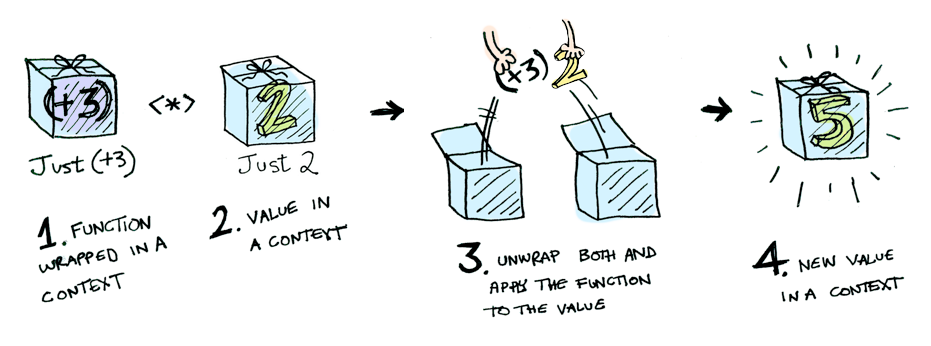
有一种省事的写法，使用<$>，它差不多是中缀的fmap

(<$>) :: (Functor f) => (a -> b) -> f a -> f b
    f <$> x = fmap f x

可以这样：

ghci> (++) <$> Just "johntra" <*> Just "volta"
Just "johntravolta"

Monoids

这玩意就是幺半群。。

幺半群是一个带有二元运算 : $M × M \rightarrow M$ 的集合 $M$ ，其符合下列公理：

结合律：对任何在 $M$ 内的$a$、$b$、$c$ ， $(a\times b)\times c = a\times (b\times c)$ 。

单位元：存在一在 $M$ 内的元素$e$，使得任一于 $M$ 内的 $a$ 都会符合 $a\times e = e\times a = a$ 。

通常也会多加上另一个公理：

封闭性：对任何在 $M$ 内的 $a$，$b$ ， $a\times b$ 也会在 $M$ 内。

单子（Monad）

我们有Maybe这种可以一次返回好多值的蛇皮类型，我们还有IO这种有副作用的猪皮类型。

那么我们现在来考虑一个问题，我需要做一件事情，而它分为几个步骤，其中每个步骤都可能失败，这意味着，我们最好用Maybe来管理数据。

举个例子：

一些例子

妖精大战争

干劲

琪露诺的斗志值。

如果Miss一次将减少100%。

在99%以下的状态时Miss，则游戏结束。

增加干劲的条件　- 冻结敌弹

　- 击伤敌人

　增加100%等价于增加一个自机，最大1000%。

我们用一个函数来表示琪露诺的干劲的变化情况，然后，为了方便，我们瞎搞一个运算符，把顺序颠倒一下

modify :: Int -> Int -> Int
modify before delta = before + delta
x -|> f = f x

这样我们就可以组合辣：

100 -|> modify 10 -|> modify -100 -|> modify 20 -|> modify -100 -|> modify 20

但是注意到琪露诺的干劲在第二次miss的时候已经不复存在了，这样算出来的是一个负数，非常不科学。

所以我们最好改改modify的类型：

modify :: Int -> Int -> Maybe Int
modify before delta 
    | before + delta > 0 = Just before + delta
    | otherwise = Nothing

然而，这给我们带来了麻烦，我们不能像上面那样组合了：我们不能把Maybe Int直接喂进Int里

不过我们可以写一大堆判断，不过。。这样丑爆。。

我们撕烤一下问题出在哪里：

Maybe可以返回多种值，导致我们不得不去分开处理它们。

所以，还是请出我们的Monad吧

Monad是个什么玩意？

class Monad m where
    return :: a -> m a
    (>>=) :: m a -> (a -> m b) -> m b
    (>>) :: m a -> m b -> m b
    
    x >> y = x >>= \_ -> y
    fail :: String -> m a
    fail msg = error msg

令人窒息。。我们可以只看前两个：return和>>=

注意到return和pure几乎是一样的，它起到包装的作用

而>>=就比较皮，它读作“bind”，它接受一个装在盒子里的值，然后把值从盒子里拿出来，应用到一个函数上，返回装在盒子里的另一个值

我们先来看下Maybe的实现好了

instance Monad Maybe where
    return x = Just x
    Nothing >>= f = Nothing
    Just x >>= f = f x
    fail _ = Nothing

对于我们比较重要的就是第四行，>>=就是对于Just x应用函数f。注意f的类型签名是f :: a -> Maybe b

回到例子

我们可以把我们的例子改成这样：

return 100 >>= modify 10 >>= modify -100

我们先用return把100包进盒子里，变成Just 100。

那把Just 100bind到modify 10是什么意思呢？

我们回头看一下bind。它将Just 100中的100从盒子中拿出来，作为参数传递给modify 10，于是我们就得到了modify 10 100这个函数，而它返回Just 110。

注意到在Maybe的Monad实现中,Nothing >>= f = Nothing，因此，如果在大战争的任意一部分出现了Nothing，结果都会是Nothing，非常科学。

另一个例子

我们xjb定义一个函数

half x = if even x
    then Just (x `div` 2)
    else Nothing

那么我们这样搞：

ghci> Just 20 >>= half >>= half >>= half
Nothing

这里同样有一张形象到爆炸的图：

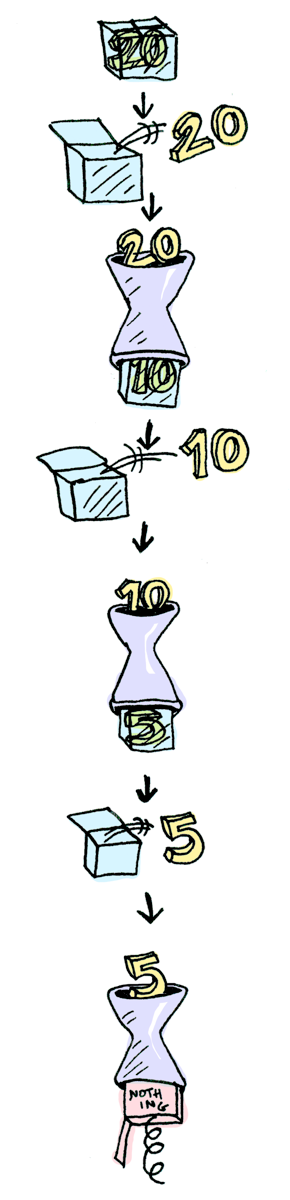
do表示法

这个东西是省事用的

foo :: Maybe String
foo = do
    x <- Just 3
    y <- Just "!"
    Just (show x ++ y)

<-实际上就是把盒子里的值取出来

还记得我们之前在哪里用do表示法吗？是IO

我们之前会这样写：

main = do
    qwq <- getline
    print qwq

因为IO是Monad，因此，qwq <- getline只是把值从IO这个盒子里取出来罢了

范畴论