[APIO2009] 抢掠计划
原题描述
题目地址:Luogu
一句话题意,有一个图,每个点都有非负点权,求从一个点开始到达若干源点的最大点权和
思路
首先考虑到如果有强连通分量,那么强连通分量内的点权是全部可以取到的,将所有强连通分量缩成一个点之后,图变成DAG,再在DAG上跑奥妙重重的SPFA最长路。最后统计一下答案就好了。
缩点
原理
即求强连通分量,使用tarjan的强连通分量算法
此处参考了byvoid的blog:有向图的强连通分量算法
考虑dfs的过程,我们维护一个$dfn$表示dfs序,维护一个栈$stk$,对于每个节点,当他进入dfs时把它放进栈中
在dfs中会有两种边,一种称之为树边,另一种为反向边(图中画风诡异的那一条),连回dfs树中的祖先。
我们维护一个对每一个节点维护一个$low$值,表示它通过反向边可以连回的最早的祖先,如图,$low(3) = 1$
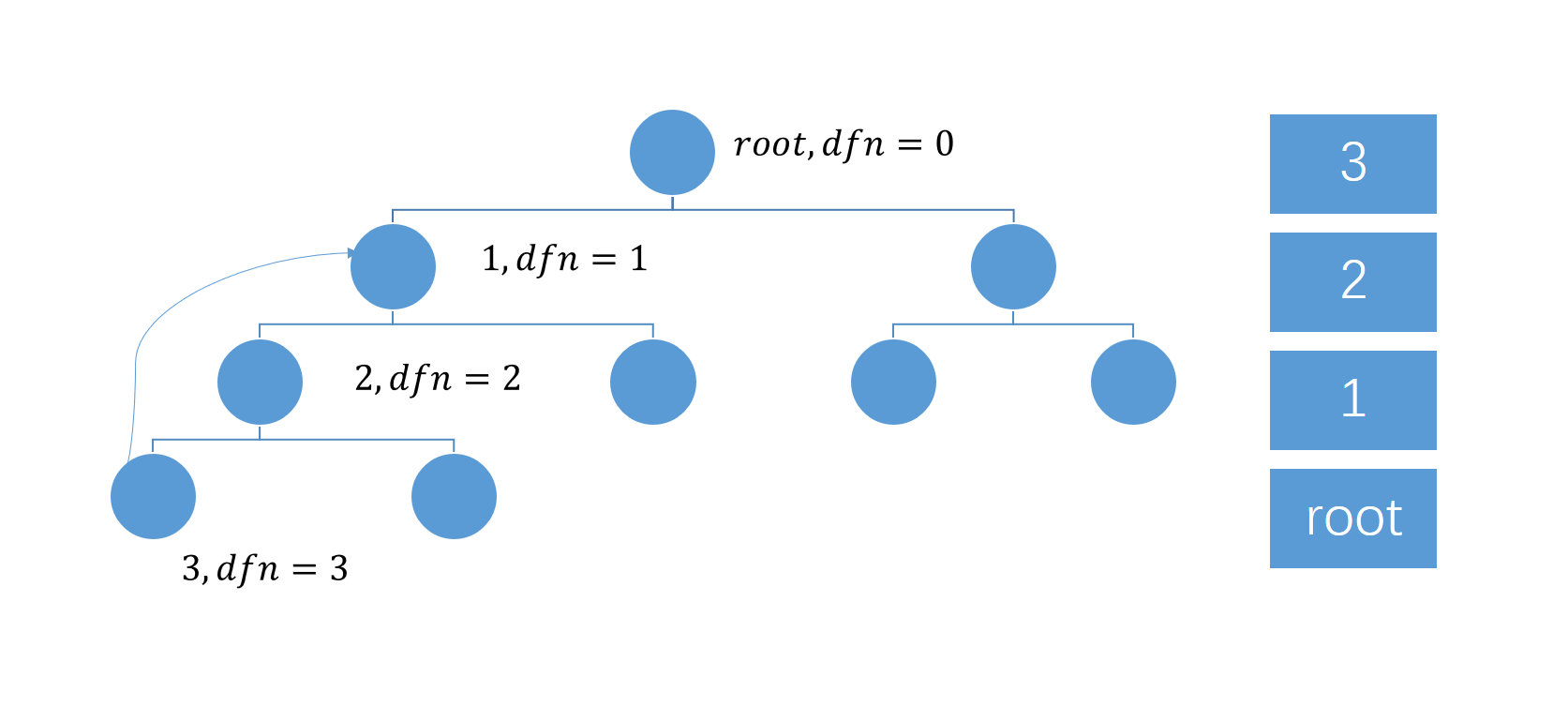
如图所示,如果继续dfs,将会回到$dfn=1$的节点,此时,在栈中,$1$号节点,到栈顶的所有点都在一个强连通分量中,这是我们把栈中的$1$号节点以上的所有点弹出,它们属于一个强连通分量。
实现
进入dfs时,首先更新$dfn,low$,然后将当前结点放入栈中。
遍历与当前节点相连的所有点,如果还没有被访问过,那么dfs它,同时更新$low$值这种情况即树边。
如果被访问过了,那么如果这个节点在栈中,即走了反向边,用这个节点的$low$值更新当前节点的$low$值。
最后如果当前节点的$low=dfn$,则当前节点一定是一个SCC在栈中最靠下的元素,即从当前节点到栈顶的所有节点都属于同一个SCC,那么弹出栈中元素,标明它们属于同一个SCC。
SPFA最长路
把松弛的地方改一下就可以了。。不过感觉比较奇特
代码
//
// Created by Margatroid on 2017/8/10.
//
#include <bits/stdc++.h>
using namespace std;
//fast read start
inline char getc()
{
static char buf[1 << 18], *fs, *ft;
return (fs == ft && (ft = (fs = buf) + fread(buf, 1, 1 << 18, stdin)), fs == ft) ? EOF : *fs++;
}
inline int gn()
{
register int k = 0, f = 1;
register char c = getc();
for (; !isdigit(c); c = getc()) if (c == '-') f = -1;
for (; isdigit(c); c = getc()) k = k * 10 + c - '0';
return k * f;
}
//fast read end
const int maxn = 500000 + 10;
vector<int> g1[maxn], g2[maxn];
void addedge(vector<int> *g, int f, int t) { g[f].push_back(t); }
bitset<maxn> instk;
int stk[maxn], low[maxn], dfn[maxn], belong[maxn], top, clk, cnt;
int w[maxn], dis[maxn], sccw[maxn];
void dfs(int no)
{
dfn[no] = low[no] = ++clk;
instk[no] = 1, stk[++top] = no;
for (int i = 0; i < g1[no].size(); ++i)
if (!dfn[g1[no][i]])
dfs(g1[no][i]), low[no] = min(low[no], low[g1[no][i]]);
else if (instk[g1[no][i]])
low[no] = min(low[no], low[g1[no][i]]);
if (dfn[no] == low[no])
for (++cnt; stk[top + 1] != no; sccw[cnt] += w[stk[top]], instk[stk[top]] = 0, --top)
belong[stk[top]] = cnt;
}
int n, m, s, p;
bitset<maxn> inq;
queue<int> que;
void spfa(int s)
{
inq[s] = 1;
que.push(s);
dis[s] = sccw[s];
while (!que.empty())
{
int u = que.front();
que.pop(), inq[u] = 0;
for (int i = 0; i < g2[u].size(); ++i)
{
if (dis[g2[u][i]] < dis[u] + sccw[g2[u][i]])
{
dis[g2[u][i]] = dis[u] + sccw[g2[u][i]];
if (!inq[g2[u][i]])
que.push(g2[u][i]), inq[g2[u][i]] = 1;
}
}
}
}
int main()
{
n = gn(), m = gn();
for (register int i = 1; i <= m; ++i)
{
register int u = gn(), v = gn();
addedge(g1, u, v);
}
for (register int i = 1; i <= n; ++i)
w[i] = gn();
s = gn(), p = gn();
for (int i = 1; i <= n; ++i)
if (!dfn[i])
dfs(i);
for (int i = 1; i <= n; ++i)
for (int j = 0; j < g1[i].size(); ++j)
if (belong[i] != belong[g1[i][j]])
addedge(g2, belong[i], belong[g1[i][j]]);
spfa(belong[s]);
int ans = 0;
for (register int i = 1; i <= p; ++i)
ans = max(ans, dis[belong[gn()]]);
cout << ans << endl;
}
navigate_before
Codeforces Round #428 (Div. 2) C
加密测试(密码是Margatroid)
navigate_next